たまには、頭の体操を。
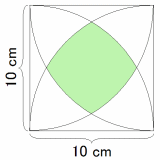
10cmの正方形の4端から、
半径10cmの円弧を描きます。
そうすると、図のような図形に
なります。
この時、緑色の部分の面積は、
いくらになるでしょうか？
中学生の時に、同じ絵で、
ラグビーボール状の部分の面積を
出す問題は、良く出題されていたかと。
この問題、中学1年くらいの頃に、
かなり苦労して解いた記憶が…。
わかった方、コメント、あるいは、トラックバックで
解答してみてくださいませ。
(8/17 1:40追記)
簡単な解法は、続きにて。
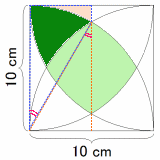まずは、赤い点線を補助線として
引きます。
2等辺三角形ができるのが
お分かりいただけるでしょう。
ということで、この線は正方形の辺を
1/2に分断します。
斜辺が10cm,短辺が5cmの
直角三角形ができてますから、
長辺(赤点線部分)は、5√3cmです。
1:2:√3の三角形だから、赤2重の角度は
30度ということになります。
あとは、青い囲みの台形の面積を出します。
(10+(10-5√3))/2*5 = 50-12.5√3
そこから30度の円弧の面積を引けば、
ピンク色部分の面積が計算できます。
50-12.5√3-100*pai*30/360
=50-12.5√3-25/3*pai
ここまで分かれば、濃緑の部分の面積も
すぐに計算できますよね。
100-100*pai*90/360-(50-12.5√3-25/3*pai)*4
=100-25*pai-200+50√3+100/3*pai
=-100+50√3+25/3*pai
最後に、ラグビーボール状の面積から
濃緑の部分2つを引けば、答えです。
(100*pai*90/360)*2-100-(-100+50√3+25/3*pai)*2
=50*pai-100+200-100√3-50/3*pai
=100/3*pai+100-100√3
=100(pai+3-3√3)/3
というわけで、概算で約31.5という答えになりますです。
コメント
円周率3.14で計算すると答えは28.5？
なにげに苦労してしまいました。
これではずれだとショック大きいです・・・
ふらぼのさん、コメントありがとうございます。
残念ですが、不正解のようですね。
円周率を3.14とすると、答えは約31.5になります。
ちなみに、ラグビーボール状の部分の面積は、約57ですね。
ヒントとしては、円弧と円弧の交点に注目です。
途中、補助線を1本引いて、台形の面積を計算したりしますですね～。
１００（π＋３－３√３）／３
で良いですよね？
http://www5a.biglobe.ne.jp/~bebeshi/main/c3/c3_005.htm
ここに書かれた解き方でいいということでしょうか？
「補助線を１本引いて」というところに引っかかっているのですが…。
nakoさん、ご名答です。
まさにその通りでございます。
何もプレゼントはございませんが、拍手をお送りいたしますです。
パチパチパチ♪
わーい (^_^)/
３０分以上かかりました（汗）
Pafuxuさん、コメントありがとうございます。
もちろん、ご指摘いただいた解法も正しいと思います。
解き方はいくつかありますからね。
要点は、内部に正三角形ができてる点ですね。
上の扇の角度が30度になってるのに気づけば、解けたも同然かと。
nakoさん、30分で解ければスゴイと思いますよ。
私が初めて解いた時は、丸一日くらい悩みましたから。
ちなみに、中学の頃の数学教師は解けませんでした。(爆)